In one of my favorite articles of 2021, Adashek et al. pointed out that even with modern expansive genomic testing, most cancer patients do not have a precision-guided option (article here, Nature Cancer 2:369, 2021). They don't have EGFR, don't have BRAF, don't have KRAS, etc. Across the field of oncology, we need more precision medicine tests, and good ones, for more patients.
Is it decisional?
Another topic is whether a precision diagnostic to guide therapy selection is strong enough to be decisional. The classic example would be a population where 50% of patients respond to Drug A. A company comes along with a new test, which effectively divides the population, by survival, on Kaplan-Meier curves, into a group with 40% response and 60% response (and p<.0001).
The issue is, oncologists tell you that they will give drug A to any patient with a 40% or better chance of response. So while Test A is a precision diagnostic, and has p<.0001, whether the patient is positive or negative on our Test A, he will still get Drug A just the same.
A payor would say that Test A lacks clinical utility. Investors upstream may have been impressed enough that the test segregates the Kaplan-Meier curve at p <.0001.
Story so far: click to enlarge the figure below.
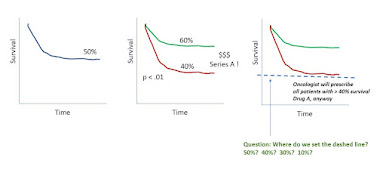 |
| click to enlarge |
There are two important points we can add, and pretty easily, to make the picture less grim for Company A. Here they come.
#1 Context Matters
Let's introduce two drugs. Drug A has an overall response rate of 50%, and Test A gives us populations with 40% or 60% response. So far, an oncologist will give every patient Drug A, due to the 40% rule.
But now let's introduce Drug B. Drug B is for the same patients, has a 50% response rate, and has no test. In a world with no test for either drug, Drug A and Drug B are a toss-up, with 50% response rate for each. In a world with Test A in use, some patients have a 60% chance of response with Drug A, so that's now better than Drug B. And some other patients have only a 40% chance of response with Drug A, so now, for those patients, Drug B becomes the better choice.
So the value of "Test A" depends entirely on the context and the choice between Drug A and Drug B.
#2 Setting a Set Point: Decision Theory; Vickers Papers
How do we make decisions which balance probabilistic pro's and con's? For example, if it takes two negative breast or prostate biopsies to find one cancer, we will go ahead with the plan of care (triggered by mammography or PSA, for example). But what if it takes 10 biopsies to find one cancer? Or 25? Or 50? Or what if an intervening test (say, a multi-kallikrein test) lets us do 4 biopsies to find 1 cancer, but, by letting more men just go home, we catch a few less total cancers. How do we draw the line?
There are better ways than hunches, hand-waving, or guessing.
Clearly, it's a form of the number-need-to-treat problem, or here, the number-needed-to-test. For me, I keep going back each year to a 2006 paper by Vickers and Elkin; Vickers is a statistician at Memorial Sloan-Kettering with a large body of work. See, "Decision Curve Analysis: A Novel Method for Evaluating Prediction Models," Med Decis Making 26:565, 2006 - here. The article models the outcomes with Treatment A with Treatment B (which might be no treatment) but can be adjusted for the expected results with and without Test A (meaning, does Test A move the needle enough to be better and different than not using Test A).
For more from Vickers, see also, "Method for evaluating prediction models," Trials 8:14, 2007 - here. See also the MSKCC website for decision curve analysis resources - here.
 |
| MSKCC interactive website |